Pavements - Falling Weight Deflectometer (FWD)
Target of Investigation
The falling weight deflectometer (FWD) (figure 1) is a nondestructive testing device widely used in pavement engineering to evaluate a pavement’s structural condition and assess its capability of handling future traffic loads. The FWD plays a crucial role in selecting optimum pavement maintenance and rehabilitation strategies. The heavyweight deflectometer (HWD) is a type of FWD that can apply a heavier load to the pavement; it is mostly used for airport airfield applications. The lightweight deflectometer is another version of the FWD that can apply a lighter load for evaluation of subgrade moduli. The light weight deflectometer (LWD) can be used to evaluate unbound bases.
 Source: FHWA.
Source: FHWA.
FWDs can be used for multiple pavement applications, including the following:
- Estimation of pavement layer moduli.
- Evaluation of a pavement’s structural condition.
- Detection of voids beneath concrete pavements.
- Determination of joint load-transfer efficiency (LTE).
The in situ estimation of parameters such as the stiffness and pavement layer moduli is necessary for assessing the condition of the pavement as a system or layer by layer. For rehabilitation purposes, FWDs can also provide information on loss of support (voids) under concrete pavements. For joint LTE testing, one of the sensors is placed behind the load plate. FWDs are used for a number of other applications that are less common but documented in the literature.(2)
Description
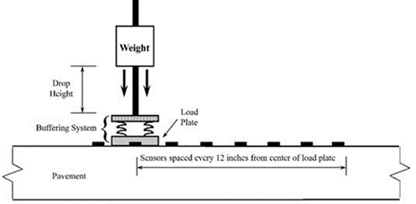
A schematic and picture of an FWD sensor configuration are shown in figure 2. The main components of the system are a machine that picks up and drops a weight, a load cell that measures the applied load, and seven or more sensors that measure the deformation of the pavement owing to the applied load.
 Source: FHWA.
Source: FHWA.
A. Schematic of an FWD sensor configuration.(2)
 © Pavement Interactive, www.pavementinteractive.org.
© Pavement Interactive, www.pavementinteractive.org.B. Photo of an FWD sensor configuration.(3)
Note: Sensors can be placed in different spacing.
By dropping a weight, an FWD generates a load pulse with a nominal duration of 30–60 ms.(2) The load pulse is transmitted to the pavement through a circular load plate that is typically
300–450 mm (12–18 inches) in diameter. The peak force that an FWD plate exerts on the pavement surface varies by the drop height and weight and can be as high as 100 kN (22 kips). An HWD can exert in excess of 300 kN (66 kips). A load cell mounted on top of the load plate measures the load imparted to the pavement surface. The outer FWD geophones are used to assess stiffness of the subgrade while those close to the center of the load measure the entire pavement response.
The load pulse deforms the pavement in the vicinity of the load plate into a shape that resembles a bowl. Sensors, such as geophones or seismometers, are mounted radially from the center of the load plate to measure pavement velocity or acceleration that is then integrated to get deflections.. The distances from the center of the load plate to the sensors are adjustable. The nominal standard sensor spacing is 300 mm (12 inches), as shown in figure 2. However, some agencies (e.g., Federal Highway Administration’s [FHWA’s] Long-Term Pavement Performance Program [LTPP]) may use different sensor configurations.(2). For joint LTE testing, one of the sensors is placed behind the load plate.
The applied force and measured deflections along the deflection bowl can be used to estimate the stiffness parameters of the pavement system as a whole or the moduli of different pavement layers and the subgrade using various computational methods.
Physical Principle
Figure 3 illustrates typical deflection responses from loading on a flexible pavement and the interior regions (i.e., those away from the joints) of a rigid pavement. The shape of the deflection bowl allows for structural analysis of the pavement. A broad bowl with little curvature indicates the pavement’s upper layers are stiff in relation to the subgrade. Conversely, a bowl with the same central deflection but a high curvature around the loading plate indicates the moduli of the upper layers are relatively low. (2)
 Source: FHWA.A. Flexible pavement.
Source: FHWA.A. Flexible pavement.
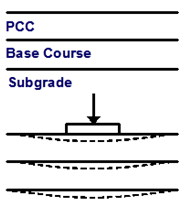 Source: FHWA.B. Rigid pavement.
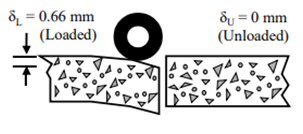
Source: FHWA.B. Rigid pavement.The response close to a crack or joint is different than those away from those elements. As shown in figure 4, the traffic load imposed on one side of a joint or crack of a rigid pavement may induce deformation on the other side because of load transfer. Both loaded and unloaded slabs deflect because a portion of the load applied to the loaded slab is transferred to the unloaded slab.(4,5)
 Source: FHWA.
Dl = loaded deflection;Du= unloaded deflection.1 mm = 0.039 inches.A. No load transfer
Source: FHWA.
Dl = loaded deflection;Du= unloaded deflection.1 mm = 0.039 inches.A. No load transfer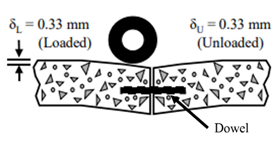 Source: FHWA.Dl = loaded deflection;Du= unloaded deflection.1 mm = 0.039 inches.
Source: FHWA.Dl = loaded deflection;Du= unloaded deflection.1 mm = 0.039 inches.B. With load transfer.
FWD testing that shows areas of high deflection at the edge of a concrete slab may be an indication of a void. Voids are generally created below slab corners because of pumping and erosion of subbase/subgrade material from repeated loading cycles.(7) Voids represent an area of poor support, which can lead to accelerated cracking and other distresses.(2)
Data Acquisition
ASTM D4694-09 and the LTPP Manual for Falling Weight Deflectometer Measurements contain procedures for performing FWD testing on pavements.(8,4) Generally, a vehicle or trailer with the FWD system is brought to a stop, and its loading plate is positioned over the test location. The deflection sensors are lowered to the pavement surface remotely. Several series of tests with the same or different nominal loads are then performed. As the load is applied to the pavement, the deflection sensors and load cell measure the load- and deflection-time histories. After the test is finished at one location, the device is moved to the next test location. A data acquisition system usually initiates data collection and storage automatically.
According to the LTPP Manual for Falling Weight Deflectometer Measurements, data for joint LTE evaluations must be collected by first placing the plate on one side of the joint and then on the other to measure the deflections on both slabs, as shown in figure 5.(4) For this application, a trailing deflection sensor (marked as D9) is necessary.
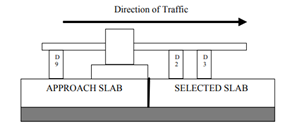 Source: FHWA.D = deflection sensor.A. Configuration for approach testing.
Source: FHWA.D = deflection sensor.A. Configuration for approach testing.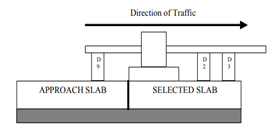 Source: FHWA.D = deflection sensor.B. Configuration for leave testing.
Source: FHWA.D = deflection sensor.B. Configuration for leave testing.For void detection, the LTPP Manual for Falling Weight Deflectometer Measurements recommends corner testing be performed in the same manner as the joint testing, except that the load plate should be tangent to both the joint or crack that defines the approach end of the slab and the longitudinal joint that defines the outside edge of the slab.(4) At least three different load levels should be used.
It is extremely important to calibrate the FWD regularly to ensure proper operation and, when an agency utilizes several FWD units, the interchangeability of data.
Data Processing
Two FHWA documents related to proper use and processing of FWD data are excellent sources of information.(2,9) FWD data processing varies with the type of pavement and the intended use of the processed data. In some cases, the process may require an experienced analyst. On this web page, data processing for the following four applications is discussed:
- Estimation of moduli of different pavement layers.
- Evaluation of a pavement’s structural condition.
- Detection of voids beneath concrete pavements.
- Determination of joint LTE.
Estimation of Moduli of Different Pavement Layers
In general terms, the estimation of layer moduli is usually carried out through a backcalculation process. Since a closed-form solution is not available for multilayer pavement systems, the backcalculation process is usually iterative. As shown in figure 6, the backcalculation process consists of assigning an initial modulus (seed value) to each layer, developing a numerical deflection basin (surface deflections at several radial distances from an applied load) from the assumed moduli, comparing the experimental and theoretical deflection basins, and adjusting the moduli of different layers iteratively until the difference between the experimental and numerical basins is below an acceptable threshold.
To implement this strategy in an automated manner, the backcalculation process consists of the following two components: an algorithm to numerically calculate the deflection basin(forward model) and an algorithm to adjust the assumed moduli to minimize the differences between the measured and calculated deflection basins (optimization algorithm).
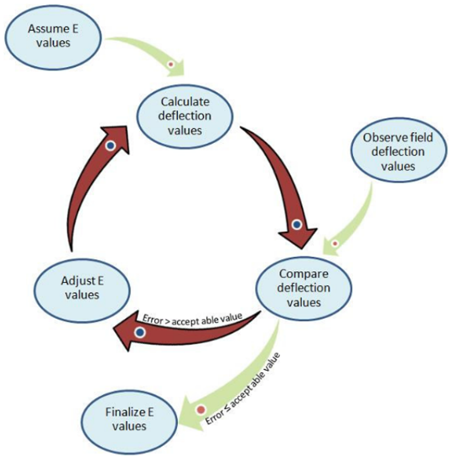
Figure 6. Illustration. Schematic diagram of a classical backcalculation process.10
The most common forward models used for flexible pavements are based on the linear-elastic layered concept. For rigid pavements, models are based on Westergaard’s solution for interior loading of a linear-elastic plate resting on a dense liquid foundation. The report Using Falling Weight Deflectometer Data with Mechanistic-Empirical Design and Analysis contains thorough explanations of these models and available software packages that implement them.(2) The LTPP Manual for Falling Weight Deflectometer Measurements mentions other advanced algorithms that consider the dynamic nature of FWD loading and the nonlinear and/or viscoelastic nature of the pavement materials.(4) These algorithms usually require the use of advanced numerical models, such as finite element models.
Most optimization or error-minimization algorithms are based on the generalized inversion technique found in many textbooks.(11) The generalized inversion technique assumes a linear relationship between perturbation in the moduli of the layers and the resulting change in the deflection basin. The partial derivative for each layer modulus estimates the change in that parameter for the next iteration. When there is a sharp contrast between the properties of two adjacent layers, nonlinear minimization techniques are conceptually preferred even though they are not as computationally efficient as the generalized inversion technique.(12) The use of artificial neural networks or genetic algorithms may also accelerate the inversion process. These approaches are effective when the profile contains only a few uniform layers.
One main concern with the backcalculation of moduli is the nonuniqueness of the solution; that is, many different combinations of layer moduli may result in almost identical deflection basins. The presence of a rigid layer or water table in shallow depths (less than 6 m [20 ft]), will negatively impact the backcalculated moduli if not taken into consideration. For these reasons, it is of utmost importance that analysts use their experience and engineering judgement.
Evaluation of a Pavement’s Structural Condition
The evaluation of a pavement structure, especially at the network level, is sometimes carried out using processes that do not require backcalculation. One method, sometimes referred to as forward calculation, assumes the pavement is a single-layer homogeneous half-space. Based on this assumption, the Boussinesq closed-form solution can be used to determine the surface modulus for each test point.(2,8) The higher the surface modulus is, the stiffer the overall pavement section will be.
Another common approach is the use of deflection indices.(13–15) Some of the more common indices are included in table 1. The appropriate use of these parameters is discussed in a number of documents, including several papers by Horak and his colleagues.(13–15)
Table 1. Deflection indices used in pavement structural evaluation.(15)
| Parameter | Formula |
| Area (A) | 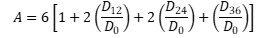 (1) (1) |
| Shape factor (F1) | 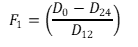 (2) (2) |
| Shape factor (F2) | 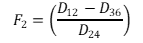 (3) (3) |
| Surface curvature index (SCI) | 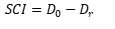 (4) (4) |
| Radius of curvature (R1) | 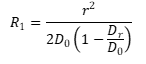 (5) (5) |
| Radius of curvature (R2) | 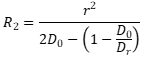 (6) (6) |
| Base curvature index (BCI) | 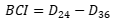 (7) (7) |
| Base damage index (BDI) | 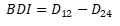 (8) (8) |
Determination of Joint LTE
The LTE of a joint is calculated via equation 9.
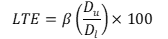 | (9) |
- Where:
- Du = deflection of the unloaded (leave) slab.
- Dl = deflection of the loaded (approach) slab.
- β = slab-bending correction factor
Parameter β is the ratio of deflection in center of loading to deflection at 12 inches (304 mm) from the center with typical values between 1.05 and 1.15; it can usually be ignored.(2) These calculations can be performed by dropping the weight on the approach side of the joint, leave side of the joint, or both.
Detection of Voids Beneath Concrete Pavements
The presence of voids is determined by measuring deflections at the slab corner using a series of load levels. As shown in figure 7, the potential for voids is determined by extrapolating the best‑fit line through the test results to determine the y-intercept (D0). The potential for the presence of voids exists when D0is greater than 0.003 inches (0.0762 mm).(16)
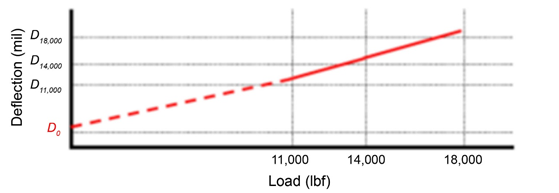 Source: FHWA.1 mil = 0.0254 mm; 1 lbf = 4.45 N.
Source: FHWA.1 mil = 0.0254 mm; 1 lbf = 4.45 N.Data Interpretation
Depending on the project, the interpretation of the processed data can be straightforward or complex. In project-level studies, the backcalculated moduli are used either directly or after adjustment to estimate the remaining pavement life or to develop a rehabilitation strategy using a design algorithm.(2,8) Because of the empirical or mechanistic–empirical nature of estimating design algorithms, adjustment factors vary from algorithm to algorithm. One should become intimately familiar with such algorithms before using the backcalculated moduli.
For network-level studies, it is more common to use measured deflections (especially central deflections), forward calculation using the Boussinesq closed-form solution, or one or more indices like those shown in table 1. These methods are usually combined with a statistical approach to categorize pavement sections by stiffness. Another use of the indices is to determine which layer in the pavement is potentially contributing to the distress. The criteria to make such analyses vary vastly among different agencies.(13–15)
Advantages
Advantages of FWDs include the following:
- Is widely used in pavement engineering to evaluate a pavement’s structural condition.
- Enables rapid, nondestructive structural evaluation of pavements.
- Provides repeatable and reproducible results with regular calibration.
Limitations
Limitations of FWDs include the following:
- Provides a nonunique solution of the backcalculated moduli, especially for multiple unknown layers.
- Requires traffic control or lane closure.
References
- Irwin, L.H., Orr, D.P., and Atkins, D. (2011). Falling Weight Deflectometer Calibration Center and Operational Improvements: Redevelopment of the Calibration Protocol and Equipment, Report No. FHWA-HRT-07-040, Federal Highway Administration, Washington, DC.
- Smith, K.D., Bruinsma, J.E., Wade, M.J., Chatti, K., Vandenbossche, J.M., and Yu, H.T. (2017). Using Falling Weight Deflectometer Data with Mechanistic-Empirical Design and Analysis, Volume I: Final Report, Report No. FHWA-HRT-16-009, Federal Highway Administration, Washington, DC.
- Pavement Tools Consortium. (n.d.) “Nondestructive Pavement Evaluation Tools.” Available online: https://www.pavementinteractive.org/nondestructive-pavement-evaluation-tools/, last accessed May 16, 2018.
- Schmalzer, P.N. (2006). LTPP Manual for Falling Weight Deflectometer Measurements, Version 4.1, Report No. FHWA-HRT-06-132, Federal Highway Administration, Washington, DC. Available online: https://rosap.ntl.bts.gov/view/dot/779, last accessed September 11, 2019.
- Khazanovich, L. and Gotlif, A. (2003). Evaluation of Joint and Crack Load Transfer Final Report, Report No. FHWA-RD-02-088, Federal Highway Administration, Washington, DC.
- Smith, K., Harrington, D., Pierce, L., Ram, P., and Smith, K. (2014). Concrete Pavement Preservation Guide, Second Edition, Report No. FHWA-HIF-14-014, Federal Highway Administration, Washington, DC.
- National Highway Institute. (1994). Pavement Deflection Analysis, Report No. FHWA‑HI‑94-021, National Highway Institute, Arlington, VA.
- ASTM D4694-09. (2015). “Standard Test Method for Deflections with a Falling‑Weight‑Type Impulse Load Device.” Book of Standards 04.03, ASTM International, West Conshohocken, PA.
- Smith, K.D., Bruinsma, J.E., Wade, M.J., Chatti, K., Vandenbossche, J.M., and Yu, H.T. (2017). Using Falling Weight Deflectometer Data with Mechanistic-Empirical Design and Analysis, Volume II: Case Study Reports, Report No. FHWA-HRT-16-009, Federal Highway Administration, Washington, DC.
- Das, A. (2010). “Interpretation of Falling Weight Deflectometer Data.” Presented at the Sealoflex World Conference, New Delhi, India.
- Santamarina, J.C. and Fratta, D. (2005). Discrete Signals and Inverse Problems: An Introduction for Engineers and Scientists, John Wiley and Sons, Chichester, United Kingdom.
- Ganji, V., Gucunski, N., and Nazarian, S. (1998). “Automated Inversion Procedure for Spectral Analysis of Surface Waves.” Journal of Geotechnical and Geoenvironmental Engineering, 8(124), pp. 757–770, American Society of Civil Engineers, Reston, VA.
- Horak, E. (1988). Aspects of Deflection Basin Parameters used in a Mechanistic Rehabilitation Design Procedure for Flexible Pavements in South Africa, Ph.D. Thesis, Department of Civil Engineering, University of Pretoria, Pretoria, South Africa.
- Horak, E. and Emery, S. (2009). “Evaluation of Airport Pavements with FWD Deflection Bowl Parameter Benchmarking Methodology.” Presented at the Second European Airport Pavement Workshop, Amsterdam, Netherlands.
- Horak, E. (2007). “Surface Moduli Determined with the Falling Weight Deflectometer Used as Benchmarking Tool.” Proceedings of the 26th Southern African Transport Conference, Pretoria, South Africa.
- Horak, E. (2007). “Surface Moduli Determined with the Falling Weight Deflectometer Used as Benchmarking Tool.” Proceedings of the 26th Southern African Transport Conference, Pretoria, South Africa.Pennsylvania Department of Transportation. Falling Weight Deflectometer, PennDOT, Harrisburg, PA. Available online: http://www.penndot.gov/ProjectAndPrograms/ResearchandTesting/RoadwayManagementandTesting/Documents/Falling%20Weight%20Deflectometer.pdf, last accessed May 4, 2018.




